SPC教程#
本文档将指导读者设置和使用统计过程控制(SPC)功能。
Info
SPC是一个单独许可的模块。
概述#
统计过程控制是一套用于监视过程的统计方法。SPC工具有助于跟踪过程行为,以便识别趋势和失控情况。当发现SPC违规时,可以触发和跟踪处理流程和纠正措施。
概念#
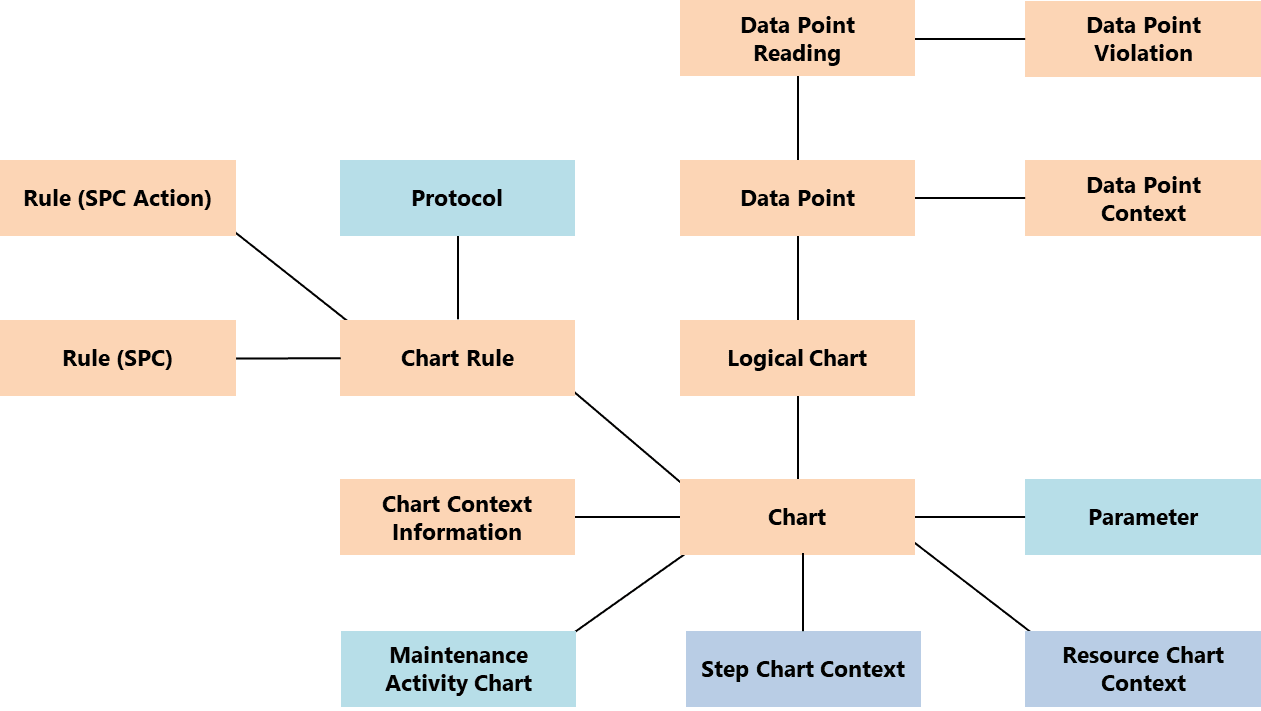
下表介绍了与SPC模块相关的主要概念。
| 术语/概念 | 描述 |
|---|---|
| 图表 | SPC图表,配置为控制特定上下文的参数。 |
| 图表键 | 将数据发布到图表时需要收集的信息,这些信息用于标识逻辑控制图。 |
| 逻辑控制图 | 图表键的每个唯一组合。 |
| 数据点 | 代表一个完整的样本。同一图表的不同数据点可能有不同的读数。 |
| 参数 | 图表中要监视的数值。 |
| 规则 | 用于评估是否发生SPC违规的逻辑。 |
| 异常流程 | 处理流程是旨在解决违规问题的工作流。 |
| 样本 | 一组收集的读数。 |
| 读数 | 参数的测量值。 |
Table: SPC主要概念
SPC对象模型是围绕着图表对象进行的,如下所示:
图表#
图表是表示SPC图表的对象。根据要控制的内容和样本大小,系统当前支持下表中列出的八种不同的图表类型。变量图表和属性图表之间的区别在于变量图表监视连续变量,通常图表会跟踪两个指标(例如:平均值和范围),而属性图表使用单个指标监视离散变量,通常与次品数有关。
| 图表名称 | 图表表示法 | 图表类型 | 数据分布 |
|---|---|---|---|
| 平均值和范围 | x̄ R | 变量 | 正常 |
| 平均值和标准偏差 | x̄ s | 变量 | 正常 |
| 中值和范围 | \(\widetilde{x}\) R | 变量 | 正常 |
| 个体和移动范围 | I-MR | 变量 | 正常 |
| 次品分数 | P | 属性 | 二项式 |
| 次品数量 | np | 属性 | 二项式 |
| 每单位次品数量 | u | 属性 | 泊松 |
| 次品数 | c | 属性 | 泊松 |
Table: 凯睿德MES SPC图表类型
接下来的小节将更详细地介绍每张图表。
平均值和范围#
下表介绍了平均值和范围图表。
| 属性 | 描述 |
|---|---|
| 图表 | 平均值和范围(x̄ R) |
| 流程观察类型 | 变量 |
| 流程观察关系 | 独立 |
| 样本大小 | < 10,但通常为3到5 |
| 分布类型 | 正常 |
| 要检测的偏移大小 | 大(≥ 1.5σ) |
| 平均值(指标1) | \(\overline{x}=\frac{\sum_i{x}_i}{n}\) |
| 范围(指标2) | \(r_{i}=Max(x_{1} \cdots x_{n})-Min(x_{1} \cdots x_{n})\) |
| 所有值的平均值 | \(\mu=\overline{\overline{X}}=\frac{\sum{x_{ij}}}{\sum{n_{i}}}\) |
| 流程平均值 | \(\mu\) |
| 流程标准偏差 | \(\sigma=S_r=\frac{\sum{r_i}\cdot\frac{\left [ d_2(n_i) \right ]}{\left [ d_3(n_i) \right ]^{2}}}{\sum{\frac{\left [ d_2(n_i) \right ]^{2}}{\left [ d_3(n_i) \right ]^{2}}}}\) 其中,\(r_i\)是数据点的范围 |
| 平均值(指标1)中心线 | \(\mu\) |
| 平均值(指标1)控制限值 | \(UCL = \mu + \frac{3\sigma}{\sqrt{n_i}}\) \(LCL = \mu - \frac{3\sigma}{\sqrt{n_i}}\) 其中,\(n_i\)是样本中的观察次数(子组) |
| 范围(指标2)中心线 | \(\overline{R_i} = d_2(n_i)\cdot\sigma\) |
| 范围(指标2)控制限值 | \(UCL = \overline{R}_i + 3\sigma \cdot d_3(n_i)\) \(LCL = max(\overline{R}_i - 3\sigma \cdot d_3(n_i);0)\) |
Table: 平均值和范围图表属性
Info
附录A - 控制图表常量中介绍了常量\(d_2\)和\(d_3\)。
平均值和标准偏差#
下表介绍了平均值和标准偏差图表。
| 属性 | 描述 |
|---|---|
| 图表 | 平均值和标准偏差(x̄ s) |
| 流程观察类型 | 变量 |
| 流程观察关系 | 独立 |
| 样本大小 | 通常>=10 |
| 分布类型 | 正常 |
| 要检测的偏移大小 | 大(≥ 1.5σ) |
| 平均值(指标1) | \(\overline{x}=\frac{\sum_i{x}_i}{n}\) |
| 标准偏差(指标2) | \(s=\sqrt{\frac{\sum(x_i-\overline{x})^2}{n-1}}\) |
| 所有值的平均值 | \(\mu=\overline{\overline{X}}=\frac{\sum{x_{ij}}}{\sum{n_{i}}}\) |
| 流程平均值 | \(\mu\) |
| 流程标准偏差 | \(\sigma=\overline{S}=\frac{\sum{S_i}\cdot\frac{c_4(n_i)}{1 - c_4(n_i)^{2}}}{\sum{\frac{c_4(n_i)^{2}}{1 - c_4(n_i)^{2}}}}\) 其中,\(S_i\)是数据点的标准偏差,计算方式如下: \(s=\sqrt{\frac{\sum(x_i-\overline{x})^2}{n-1}}\) |
| 平均值(指标1)中心线 | \(\mu\) |
| 平均值(指标1)控制限值 | \(UCL = \mu + \frac{3\sigma}{\sqrt{n_i}}\) \(LCL = \mu - \frac{3\sigma}{\sqrt{n_i}}\) |
| 标准偏差(指标2)中心线 | \(\overline{S}_i = c_4(n_i)\cdot\sigma\) |
| 标准偏差(指标2)控制限值 | \(UCL = \overline{S}_i + 3\sigma \cdot c_5(n_i)\) \(LCL = max(\overline{S}_i - 3\sigma \cdot c_5(n_i);0)\) |
Table: 平均值和标准偏差图表属性
Info
附录A - 控制图表常量中介绍了常量\(c_4\)和\(c_5\)。
中值和范围#
下表介绍了中值和范围图Table:
| 属性 | 描述 |
|---|---|
| 图表 | 中值和范围(\(\widetilde{X}\) R) |
| 流程观察类型 | 变量 |
| 流程观察关系 | 独立 |
| 样本大小 | < 10,但通常为3到5 |
| 分布类型 | 正常 |
| 要检测的偏移大小 | 大(≥ 1.5σ) |
| 中值(指标1) | \(\widetilde{X}\) = 可以通过从最低值到最高值排列所有观察值并选择中间值,来找到有限数字列表的中值。如果有偶数个观察值,则中值是两个中间值的平均值。 |
| 范围(指标2) | \(r_{i}=Max(x_{1} \cdots x_{n})-Min(x_{1} \cdots x_{n})\) |
| 流程平均值 | \(\mu=\overline{\widetilde{X}}=\frac{\sum{\widetilde{x_{i}}}}{n}\) |
| 流程标准偏差 | \(\sigma=S_r=\frac{\sum{r_i}\cdot\frac{\left [ d_2(n_i) \right ]}{\left [ d_3(n_i) \right ]^{2}}}{\sum{\frac{\left [ d_2(n_i) \right ]^{2}}{\left [ d_3(n_i) \right ]^{2}}}}\) 其中,\(r_i\)是数据点的范围 |
| 中值(指标1)中心线 | \(\overline{\widetilde{X}}=\mu\) |
| 中值(指标1)控制限值 | \(UCL = \mu + \frac{3\sigma\cdot e1}{\sqrt{n_i}}\) \(LCL = \mu - \frac{3\sigma\cdot e1}{\sqrt{n_i}}\) |
| 范围(指标2)中心线 | \(\overline{R_i} = d_2(n_i)\cdot\sigma\) |
| 范围(指标2)控制限值 | \(UCL = \overline{R}_i + 3\sigma \cdot d_3(n_i)\) \(LCL = max(\overline{R}_i - 3\sigma \cdot d_3(n_i);0)\) |
Table: 中值和范围图表属性
Info
附录A - 控制图表常量中介绍了常量\(d_2\)、\(d_3\)和\(e_1\)。
个体和移动范围#
下表介绍了个体和移动范围图Table:
| 属性 | 描述 |
|---|---|
| 图表 | 个人和移动范围(I-MR) |
| 流程观察类型 | 变量 |
| 流程观察关系 | 独立 |
| 样本大小 | 1 |
| 分布类型 | 正常 |
| 要检测的偏移大小 | 大(≥ 1.5σ) |
| 个人(指标1) | \(x\) |
| 移动范围(指标2) | \(r_i = Abs(x_{i}-x_{i-1})\) |
| 平均值 | \(\mu = \overline{\overline{x}} = \frac{\sum{x_i}}{n}\) |
| 平均值范围 | \(\overline{MR} = \frac{\sum{MR_i}}{i-1}\) |
| 流程平均值 | \(\mu\) |
| 流程标准偏差 | \(\sigma = S_{mr} = \frac{\overline{MR}}{d_2(w)}\) 因为\(w=2\),\(d_2(w)\)可以替换为常量 1.1284其中\(\overline{MR} = \frac{\sum{MR_i}}{i-1}\) 请注意,第一个数据点没有 \(MR\) |
| 个人(指标1)中心线 | \(\mu\) |
| 个人(指标1)控制限值 | \(UCL = \mu + 3 \sigma\) \(LCL = \mu - 3 \sigma\) |
| 移动范围(指标2)中心线 | \(\overline{MR_i} = \sigma\cdot d_2(w)\) |
| 移动范围(指标2)控制限值 | \(UCL = \overline{MR_{i}} + 3\sigma \cdot d_3(w)\) \(LCL = max(\overline{MR}_i + 3\sigma \cdot d_3(w);0)\) 其中 \(w=2\) |
Table: 个人和移动范围图表属性
Info
附录A - 控制图表常量中介绍了常量\(d_2\)和\(d_3\)。
次品分数#
下表介绍了次品分数图Table:
| 属性 | 描述 |
|---|---|
| 图表 | 次品率(p) |
| 流程观察类型 | 属性 |
| 流程观察关系 | 独立 |
| 样本大小 | 变量,通常>=50 |
| 分布类型 | 二项式 |
| 要检测的偏移大小 | 大(≥ 1.5σ) |
| 次品率(指标1) | \(p=\frac{number\;of\;rejects}{number\;inspected}\) |
| 指标2 | 不适用 |
| 样本的标准偏差 | \(s = \sqrt{\frac{\overline{p}(1-\overline{p})}{n}}\) 其中,\(\overline{p}\)是中心线,\(n\)是样本大小,可能因样本而异 |
| 次品率(指标1)中心线 | \(\overline{p}=\frac{total\;number\;of\;rejects}{total\;number\;inspected}\) |
| 次品率(指标1)控制限值 | \(UCL = min(\overline{p}+3s;1)\) \(LCL = max(\overline{p}-3s;0)\) |
| 指标2中心线 | 不适用 |
| 指标2控制限值 | 不适用 |
Table: 次品率图表属性
次品数量#
下表介绍了次品数量图Table:
| 属性 | 描述 |
|---|---|
| 图表 | 次品数量(np) |
| 流程观察类型 | 属性 |
| 流程观察关系 | 独立 |
| 样本大小 | 常量,通常为\>=50 |
| 分布类型 | 二项式 |
| 要检测的偏移大小 | 大(≥ 1.5σ) |
| 次品数量(指标1) | \(p=number\;of\;rejects\) |
| 指标2 | 不适用 |
| 样本的标准偏差 | \(s = \sqrt{n\overline{p}\left ( 1-\frac{n\overline{p}}{n} \right )}\) 其中,\(n\overline{p}\)是中心线,\(n\)是样本大小,其是常量 |
| 次品数量(指标1)中心线 | \(n\overline{p}=\frac{total\;number\;of\;rejects}{number\;of\;samples}\) |
| 次品数量(指标1)控制限值 | \(UCL = n\overline{p} + 3s\) \(LCL = max(n\overline{p}-3s;0)\) |
| 指标2中心线 | 不适用 |
| 指标2控制限值 | 不适用 |
Table: 次品数量图表属性
每单位次品数量#
下表介绍了每单位次品数量图Table:
| 属性 | 描述 |
|---|---|
| 图表 | 每单位次品数量(u) |
| 流程观察类型 | 属性 |
| 流程观察关系 | 独立 |
| 样本大小 | 变量 |
| 分布类型 | 泊松 |
| 要检测的偏移大小 | 大(≥ 1.5σ) |
| 每单位次品数量(指标1) | \(u =\frac{number\;of\;defects}{sample\;size}\) |
| 指标2 | 不适用 |
| 标准偏差 | \(s = \sqrt{\frac{\overline{u}}{n}}\) 其中,\(\overline{u}\)是中心线,\(n\)是样本大小,可能因样本而异 |
| 每单位次品数量(指标1)中心线 | \(\overline{u}=\frac{c_1+c_2+\cdots+c_i}{n_1+n_2+\cdots+n_i}\) 其中,c是每个样本的次品数量,n是样本大小 |
| 每单位次品数量(指标1)控制限值 | \(UCL=\overline{u}+3s\) \(LCL = max(\overline{u}-3s;0)\) |
| 指标2中心线 | 不适用 |
| 指标2控制限值 | 不适用 |
Table: 每单位次品数量图表属性
次品数#
下表介绍了次品数图Table:
| 属性 | 描述 |
|---|---|
| 图表 | 次品数量(c) |
| 流程观察类型 | 属性 |
| 流程观察关系 | 独立 |
| 样本大小 | 常量 |
| 分布类型 | 泊松 |
| 要检测的偏移大小 | 大(≥ 1.5σ) |
| 次品数量(指标1) | \(c=number\;of\;defects\) |
| 指标2 | 不适用 |
| 标准偏差 | \(s = \sqrt{\overline{c}}\) 其中,\(\overline{c}\)是中心线 |
| 次品数量(指标1)中心线 | \(\overline{c}=\frac{c_1+c_2+\cdots+c_i}{i}\) 其中,c是每个样本的次品数量 |
| 次品数量(指标1)控制限值 | \(UCL=\overline{c}+3s\) \(LCL = max(\overline{c}-3s;0)\) |
| 指标2中心线 | 不适用 |
| 指标2控制限值 | 不适用 |
Table: 次品数量图表属性
逻辑控制图#
图表由许多逻辑控制图组成。系统会自动为图表上下文键的每个唯一组合创建逻辑控制图。例如,如果要在十个设备(资源)上监视一个参数,则不必创建十个不同的图表;只需创建一个图表并将资源定义为图表上下文键。这种机制允许在步骤、设备(资源)、产品等之间重用相同的图表。图表可以有许多上下文键。除上下文键外,图表还可以定义其他强制性上下文信息。始终可以提供非强制性上下文。
当逻辑控制图首次创建时(通过将数据发布到特定上下文键组合或显式创建),系统将自动创建逻辑控制图,继承在图表级别定义的所有属性。但是,每个逻辑控制图都将保留一组自己的属性,如下表所示:
| 属性 | 描述 |
|---|---|
| 规格下限 | 规格下限 |
| 规格目标值 | 规格目标值 |
| 规格上限 | 规格上限 |
| 指标1中心线 | 指标1中心线(如果控制限值是自动的,则从该中心线计算控制限值) |
| 指标2中心线 | 指标2中心线 |
| 标准偏差 | 标准偏差 |
| Y轴刻度 | Y轴刻度是手动还是自动 |
| Y轴最小值 | 如果Y轴刻度为手动,最小值 |
| Y轴最大值 | 如果Y轴刻度为手动,最大值 |
| Y轴主要单位 | 如果Y轴刻度为手动,刻度之间的距离 |
| 数据点计数器 | 在内部用于计算数据点的数量 |
| 使用自动控制限值 | 是否使用自动控制限值 |
| 处于学习模式 | 学习模式是否处于活动状态 |
| 禁用学习后自动计算控制限值 | 学习后是否不再重新计算控制限值 |
| 自动计算控制限值指标 | 控制限值是否会自动重新计算 |
| 自动计算计数器 | 在内部用于计算数据点的数量,直到必须重新计算控制限值(如果启用了重新计算中心线的选项) |
Table: 逻辑控制图属性
图表统计信息#
下面介绍的图表统计信息是根据在逻辑控制图GUI中可见的所有数据点进行计算的,计算时不包括已删除和已排除的数据点。所有公式仅适用于指标1。
某些图表统计信息对规格限制和控制限值使用单一值。由于规格限制(下限、目标、上限)以及中心线和控制限值(控制下限和控制上限)可能会因数据点而异,因此将根据配置条目Cmf/System/Configuration/SPC/MultipleDataPointsStatistics/CalculationMode/中定义的值处理这些值的变化,该条目可以有两个值:
- 平均值(默认值,没有值时使用)- 使用所考虑数据点的平均值(默认值)。所考虑数据点仅包含所需值(规格下限、规格目标值、规格上限、控制下限、中线和控制上限)。
- 最后 - 如果为数据点定义了值,则使用最后一个数据点的值(规格下限、规格目标值、规格上限、控制下限、中心线和控制上限)。
| 指标 | 公式 | 数据点 | 读数 | 显示 | 注意 |
|---|---|---|---|---|---|
| 计数 | 计数 | x | 所有图表 | 所有数据点 | |
| 最大 | 最大值 | x | 所有图表 | ||
| 最小 | 最小值 | x | 所有图表 | ||
| 平均值 | \(\overline{x}=\frac{x_1+x_2+x_3+\cdots+x_n}{n}\) | x | 所有图表 | ||
| 总体平均值 | \(\mu=\frac{x_1+x_2+x_3+\cdots+x_n}{n}\) | x | 未显示 | 此指标考虑所有单个读数,不包括聚合的数据点 | |
| 标准偏差 | \(s=\sqrt{\frac{\sum(x_i-\overline{x})^2}{n-1}}\) | x | 所有图表(当数据点> 1时) | ||
| 总体标准偏差 | \(\delta=\sqrt{\frac{\sum(x_i-\overline{x})^2}{n-1}}\) | x | 未显示 | 此指标考虑所有单个读数,不包括聚合的数据点 | |
| 中值 | \(\widetilde{x}\) | x | 所有图表 | 可以通过从最低值到最高值排列所有观察值并选择中间值,来找到有限数字列表的中值。如果有偶数个观察值,则中值是两个中间值的平均值。 | |
| 范围 | \(Range=Max(x_{1\cdots n})-Min(x_{1\cdots n})\) | x | 所有图表 | ||
| 组内标准偏差 | 对于个人和移动范围图Table: \(\hat{\delta}_{Within}=\frac{\overline{MR}}{d2(w)}\) 其中,w=2时\(d2(w)\)为 1.1284。对于其他类型的变量图表,合并标准偏差(SP)是根据以下公式计算的: \(S_p=\sqrt{\frac{\left [ \sum_{i}\sum_{j}{(X_{ij} - \overline{X_i})^2} \right ]}{\left [ \sum_{i}{(n_{i} - 1} \right ]}}\) 然后,自由度(d)的计算公式为: \(\sum(n_i-1)\) 最后,使用以下公式计算组内标准偏差: \(\hat{\delta}_{Within}=\frac{Sp}{c4(d+1)}\) | x | x | 未显示 | |
| Cp - 流程能力 | \(C_p=\frac{USL-LSL}{6\hat{\delta}_{Within}}\) | x | x | 所有变量图表(当数据点> 1时) | 关于要考虑的数据点 – 如果更改或丢失USL/LSL,请参阅本文档前面所述的计算模式。 |
| Cp,upper - 上线流程能力 | \(C_{p,upper}=\frac{USL-\mu}{3\hat{\delta}_{Within}}\) \(\mu\) 要使用的是所考虑数据点的所有单独读数的总体平均值 – 与Pp相同 | x | x | 未显示 | 关于要考虑的数据点 – 如果更改或丢失USL/LSL,请参阅本文档前面所述的计算模式。此指标考虑所有单个读数,不包括聚合的数据点。 |
| Cp,lower - 下线流程能力 | \(C_{p,lower}=\frac{\mu-LSL}{3\hat{\delta}_{Within}}\) \(\mu\) 要使用的是所考虑数据点的所有单独读数的总体平均值 – 与Pp相同 | x | x | 未显示 | 从不显示 – 用于以后的计算;关于要考虑的数据点 – 如果更改或丢失USL/LSL,请参阅本文档前面所述的计算模式。 此指标考虑所有单个读数,不包括聚合的数据点。 |
| Cpk - 流程能力指数 | \(C_{pk}=min(C_{p,lower},C_{p,upper})\) | x | x | 所有变量图表(当数据点> 1时) | 如果是单面,系统只考虑方程式中不可为空的部分 |
| Z-Score - 标准评分 | \(Z=3C_{pk}\) | x | x | 所有变量图表(当数据点> 1时) | 1 |
| Pp- 流程绩效 | \(P_p=\frac{USL-LSL}{6\delta}\) | x | x | 所有变量图表(当数据点> 1时) | 关于要考虑的数据点 – 如果更改或丢失USL/LSL,请参阅本文档前面所述的“计算模式”。此指标不包括所有聚合的数据点。 |
| Pp,upper | \(P_{p,upper}=\frac{USL-\mu}{3\delta}\) | x | x | 未显示 | 关于要考虑的数据点 – 如果更改或丢失USL/LSL,请参阅本文档前面所述的“计算模式”。此指标不包括所有聚合的数据点。 |
| Pp,lower | \(P_{p,lower}=\frac{\mu-LSL}{3\delta}\) | x | x | 未显示 | |
| PPK – 流程绩效指数 | \(P_{pk}=min(P_{p,lower},P_{p,upper})\) | x | x | 所有变量图表(当数据点> 1时) | 注意:如果是单面,系统只考虑方程式中不可为空的部分 |
| OOS – 超出规格 | 计算高于规格上限或低于规格下限的所有数据点的所有读数的数量。 | x | 所有图表 | ||
| OOC – 失控 | 计算高于控制上限或低于控制下限的数据点数。 | x | 所有图表 | 对于变量图表,此指标仅考虑指标1 | |
| OOC% - 失控率 | \(OOC(\%)=100\%\frac{OOC}{number\;of\;data\;points}\) | x | 所有图表 | ||
| OTI – 符合目标指标 | \(OTI=\frac{\overline{x}-Target\;Spec\;Value}{s}\) | x | 所有变量图表(当数据点> 1时) | 2 | |
| OCI – 符合中心指标 | \(OCI=\frac{\overline{x}-Centerline}{s}\) | x | 所有变量图表(当数据点> 1时) | 3 | |
| LCLCR – 控制下限变化比率 | \(LCLCR=\frac{LCL-(\overline{x}-3s)}{s}\) | x | 所有变量图表(当数据点> 1时) | 4 | |
| UCLCR – 控制上限变化比率 | \(UCLCR=\frac{(\overline{x}+3s)-UCL}{s}\) | x | 所有变量图表(当数据点> 1时) | 5 | |
| CLCR – 控制限值变化比率 | if \(abs(LCLCR)\) > \(abs(UCLCR)\) \(CLCR=LCLCR\) else \(CLCR=UCLCR\) | x | 所有变量图表(当数据点> 1时) | 6 |
Table: 图表统计信息
Note
1 仅当配置条目/Cmf/System/Configuration/SPC/ChartStatistics/IncludeZScore设置为以下内容时才会显示: true
Note
2 仅当配置条目/Cmf/System/Configuration/SPC/ChartStatistics/IncludeOTISection设置为true时才会显示。关于要考虑的数据点 – 如果更改或丢失目标规格值,请参阅本文档前面所述的计算模式。
Note
3 仅当配置条目/Cmf/System/Configuration/SPC/ChartStatistics/IncludeOTISection设置为true时才会显示。关于要考虑的数据点 – 如果更改中心线值,请参阅本文档前面所述的计算模式。
Note
4 仅当配置条目/Cmf/System/Configuration/SPC/ChartStatistics/IncludeCLRSection设置为true时才会显示。关于要考虑的数据点 – 如果更改LCL,请参阅本文档前面所述的计算模式。
Note
5 仅当配置条目/Cmf/System/Configuration/SPC/ChartStatistics/IncludeCLRSection设置为true时才会显示。关于要考虑的数据点 – 如果更改UCL,请参阅本文档前面所述的计算模式。
Note
6 仅当配置条目/Cmf/System/Configuration/SPC/ChartStatistics/IncludeCLRSection设置为以下内容时才会显示: true
数据点#
每次向SPC发布数据时,都会创建数据点。数据点存储了许多属性,包括作为数据点一部分的读数。下表显示了最重要的属性。
| 属性 | 描述 |
|---|---|
| 状态 | 数据点的状态: - 活动 - 已删除 - 已编辑 - 已排除 |
| 读数数量 | 读数的数量 |
| 读数值 | 单个读数值 |
| 样本大小 | 样本大小 |
| 注释 | 数据点被标注的注释(如有) |
| 值1 | 数据点的指标1的值 |
| 值2 | 数据点的指标2的值 |
| 规格上限 | 应用于数据点的规格上限 |
| 规格目标值 | 应用于数据点的目标规格值 |
| 规格下限 | 应用于数据点的规格下限 |
| 控制上限1 | 应用于数据点时指标1的控制上限 |
| 中心线1 | 应用于数据点时指标1的中心线 |
| 控制下限1 | 应用于数据点时指标1的控制下限 |
| 控制上限2 | 应用于数据点时指标2的控制上限 |
| 中心线2 | 应用于数据点时指标2的中心线 |
| 控制下限2 | 应用于数据点时指标2的控制下限 |
Table: 数据点属性
Note
中心线2取决于标准偏差的值。重新计算控制限值时,会计算标准偏差的值,而不是中心线2。
数据点的状态会产生不同的图形表示,它对如何考虑统计数据和SPC规则有影响,如下表所示:
| 状态 | Active | 已编辑 | 已排除 | 已删除 |
|---|---|---|---|---|
| 在图表中可见 | x | x | x | |
| 用于直方图和统计数据 | x | x | ||
| 在SPC规则中考虑 | x | x | ||
| 用于中心线重新计算 | x | x |
Table: 数据点状态影响
点统计信息#
下表介绍了GUI中显示的点统计数据。统计数据是基于单个数据点计算的,考虑到所有数据点读数,仅适用于变量图表。
| 指标 | 公式 | 显示 |
|---|---|---|
| 计数 | 计数 | 所有变量图表 |
| 最大 | 最大值 | 所有变量图表 |
| 最小 | 最小值 | 所有变量图表 |
| 平均值 | \(\overline{x}=\frac{x_1+x_2+x_3+\cdots+x_n}{n}\) | 所有变量图表 |
| 标准偏差 | \(s=\sqrt{\frac{\sum(x_i-\overline{x})^2}{n-1}}\) | 读数大于1时的所有变量图表 |
| 中值 | \(\widetilde{x}\)= 可以通过从最低值到最高值排列所有观察值并选择中间值,来找到有限数字列表的中值。如果有偶数个观察值,则中值是两个中间值的平均值。 | 所有变量图表 |
| 范围 | \(Range=Max(x_{1\cdots n})-Min(x_{1\cdots n})\) | 所有变量图表 |
| Cp流程能力 | \(C_p=\frac{USL-LSL}{6s}\) 注意:晋档数据点存在USL和LSL时,才计算此值。 | 读数大于1时的所有变量图表 |
| Cpk流程能力指数 | \(Min(\frac{USL-\overline{x}}{3s},\frac{\overline{x}-LSL}{3s})\) | 读数大于1时的所有变量图表 |
| Cir | \(Cir=\frac{3\cdot \sqrt{(\overline{x}-TSV)^2+s^2}}{Min(USL\;-\;TSV,\;TSV-LSL)}\) 其中\(TSV\)=TargetSpectValue | 读数大于1时的所有变量图表 |
Table: 点统计信息
步骤和资源图表上下文#
图表可以分别通过步骤图表上下文和资源图表上下文附加到步骤或资源。这些上下文的目的是:
- 根据物料或资源上下文解析SPC图表的使用权利
- 启用自动EDC数据馈送至SPC
步骤图表上下文可以按照下表中所述进行定义:
| 属性 | 可选 | 类型 | 备注 |
|---|---|---|---|
| 步骤 | 否 | 键 | |
| 产品 | 是 | 键 | |
| 产品组 | 是 | 键 | |
| 流程 | 是 | 键 | |
| 物料类型 | 是 | 键 | |
| 资源 | 是 | 键 | |
| 资源类型 | 是 | 键 | |
| 模型 | 是 | 键 | |
| 操作 | 是 | 键 | 支持的操作包括: - TrackIn -- 用于进站 - TrackOut -- 用于出站 - PerformImmediate -- 用于执行即时数据采集 - MoveNext -- 用于迁移至下一站 - Rework -- 用于返工 - PerformSetup 用于执行设置 |
| 图表 | 否 | 值 | |
| 显示模式 | 否 | 值 | 支持的模式包括: - AcknowledgeAlways -- 每次都需要用户的明确确认 - AcknowledgeOnViolationsOnly -- 仅当检测到违规时才需要用户明确确认 - DisplayAlways -- 每次都会显示图表 - DisplayOnViolationsOnly -- 仅在发生违规时显示图表 - None -- 从不显示图表 |
Table: 步骤图表上下文
为资源的状态转换定义的资源图表上下文,如下表所述:
| 属性 | 可选 | 类型 | 备注 |
|---|---|---|---|
| 资源 | 是 | 键 | |
| 资源类型 | 是 | 键 | |
| 模型 | 是 | 键 | |
| 状态转换 | 否 | 键 | 状态转换在查找表 ResourceChartStateTransitions 中定义 |
| 图表 | 否 | 值 | |
| 显示模式 | 否 | 值 | 支持的模式与步骤图表上下文中所述的相同。 |
Table: 资源图表上下文
Info
对于步骤图表上下文和资源图表上下文,同一个上下文组合可以有多张图表。
SPC规则#
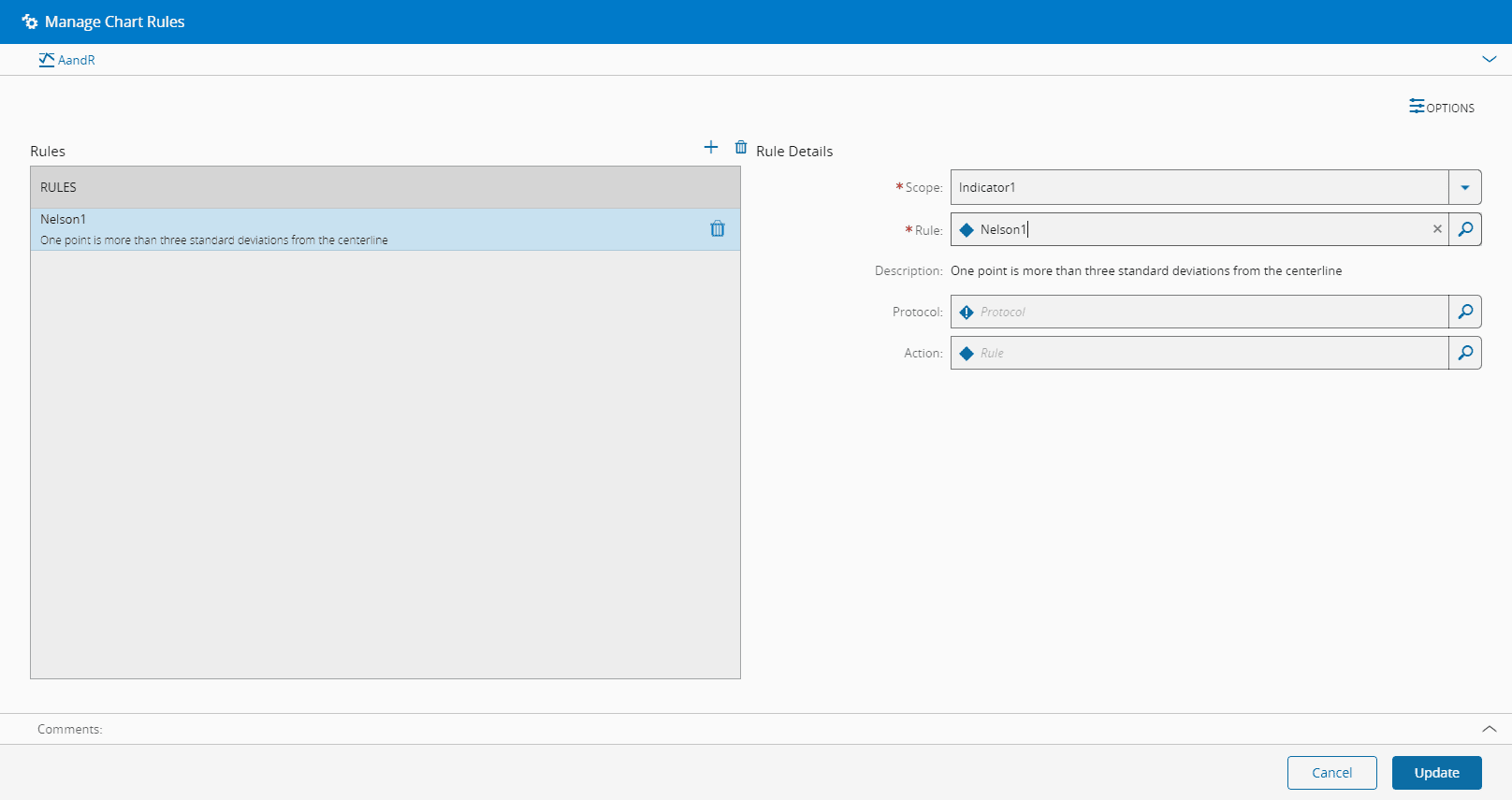
SPC规则用于检测SPC违规。图表可以有许多SPC规则。SPC规则测试特定模式的特定指标。还可以为每个图表SPC规则指定要打开的异常流程,以及在检测到该SPC规则模式时自动执行的操作。
SPC规则可以是系统规则或用户定义的规则。系统规则基于规格限制以及Nelson和Western Electric规则,下表中介绍了这些规则。
| 规则名称 | 描述 |
|---|---|
| OutOfSpec | 任何高于规格上限(如果已定义)或低于规格下限(如果已定义)的读数 |
| Nelson1 | 高于+3西格玛或低于-3西格玛的1个点(共1个点)(与WesternElectric1相同) |
| Nelson2 | 中心线同一侧的9个点(共9个点)(类似于WesternElectric4,具有9个点而不是8个点) |
| Nelson3 | 6个连续递增或递降点 |
| Nelson4 | 14个连续交替点 |
| Nelson5 | 中心线同一侧高于+2西格玛或低于-2西格玛的2个连续点(共3个点) |
| Nelson6 | 中心线同一侧高于4西格玛或低于-1西格玛的+1个连续点(共5个点) |
| Nelson7 | 中心线两侧连续15个交替点 |
| Nelson8 | 中心线两侧介于+1和-1西格玛之间的8个连续点 |
| WesternElectric1 | 高于+3西格玛或低于-3西格玛的1个点(共1个点) |
| WesternElectric2 | 中心线同一侧高于+2西格玛或低于-2西格玛的2个连续点(共3个点) |
| WesternElectric3 | 中心线同一侧高于4西格玛或低于-1西格玛的+1个连续点(共5个点) |
| WesternElectric4 | 中心线同一侧的8个点(共8个点) |
Table: 系统SPC规则
SPC规则对指标以及特定图表或图表类型的适用性由通用表ChartRuleScope提供。默认情况下,系统附带的配置如下所示。
| 规则 | 指标范围 | 范围类型 | 图表类型 | 图表 |
|---|---|---|---|---|
| OutOfSpec | Indicator1 | 全部 | ||
| Nelson 1 | Indicator1And2 | 全部 | ||
| Nelson 2 | Indicator1And2 | 全部 | ||
| Nelson 3 | Indicator1And2 | 全部 | ||
| Nelson 4 | Indicator1And2 | 全部 | ||
| Nelson 5 | Indicator1 | 图表类型 | 变量 | |
| Nelson 6 | Indicator1 | 图表类型 | 变量 | |
| Nelson 7 | Indicator1 | 图表类型 | 变量 | |
| Nelson 8 | Indicator1 | 图表类型 | 变量 | |
| Western Electric 1 | Indicator1And2 | 全部 | ||
| Western Electric 2 | Indicator1 | 图表类型 | 变量 | |
| Western Electric 3 | Indicator1 | 图表类型 | 变量 | |
| Western Electric 4 | Indicator1And2 | 全部 |
Table: 用于范围解析的默认通用表ChartRuleScope配置
点选择#
在计算SPC规则时,只应考虑尚未删除或排除的点。此外,如果/Cmf/System/Configuration/SPC/ChartRules/FilterByControlLimits的配置值设置为True,则在选择可计入规则计算的点时必须,考虑以下事项:
对于所有图Table:
- 只考虑中心线1的值与最后一个点相同的点。
对于变量图Table:
- 如果最后一个点的标准偏差值不为空,则仅考虑标准偏差值与最后一个点相同的点;
- 如果最后一个点的标准偏差值不为空,则仅考虑中心线2的值与最后一个点相同的点;
Note
如果是手动计算,则值可以为空
区域#
SPC规则中提到的西格玛区域始终基于中心线和控制限值,无论这些限值是手动定义还是自动定义,如下图所示。上西格玛区域的计算方法是将控制上限和中心线之间的差除以三。相反,下西格玛区域的计算方法是将中心线和控制下限之间的差除以三。
Info
可以通过自定义来扩展SPC规则列表,方法是创建新的DEE操作并将其链接到范围SPC的规则对象。有关如何开发自定义SPC规则的详细信息,请参阅《开发人员指南》。
SPC操作#
可以定义违反SPC规则时要触发的SPC操作。例如,可以扣留物料,释放设备,请求维保,发送警报或发送电子邮件。系统自带三个SPC操作,如下表所示,但可以创建任何所需的SPC操作。有关如何创建SPC操作的信息,请参阅《开发人员指南》。
| 规则名称 | 描述 |
|---|---|
| SPCHoldMaterial | 如果物料是数据点上下文信息的一部分,此操作将在当前的物料步骤中查找尚未分配给物料的第一个扣留(按字母顺序排序)原因,并处于此特定原因扣留物料。 |
| SPCPutEquipmentDown | 如果资源是数据点上下文信息的一部分,并且该资源有与其关联的状态模型,则此操作将查找第一个状态模型状态(按字母顺序排序),其属性SEMI-E10为“非计划停机”,它将把该资源的状态调整为该特定状态。 |
| SPCSendMail | 此操作将向配置条目中定义的分布列表发送一封电子邮件,内容是关于图表和违规的信息:/Cmf/System/Configuration/Mail/LocalSupport/ |
Table: 系统SPC操作
Info
SPC操作必须是范围SPPCAction的规则对象。
控制限值#
控制限值 - 控制上限(UCL)和控制下限(LCL) - 是过程的呼声(VOP),通常在SPC术语中称为UAL(操作上限)和LAL(操作下限)。控制限值因图表类型而异。在某些情况下,它们在一段时间内是固定的,而在其他情况下,它们是可变的(以考虑到样本大小的差异)。
自动和手动控制限值#
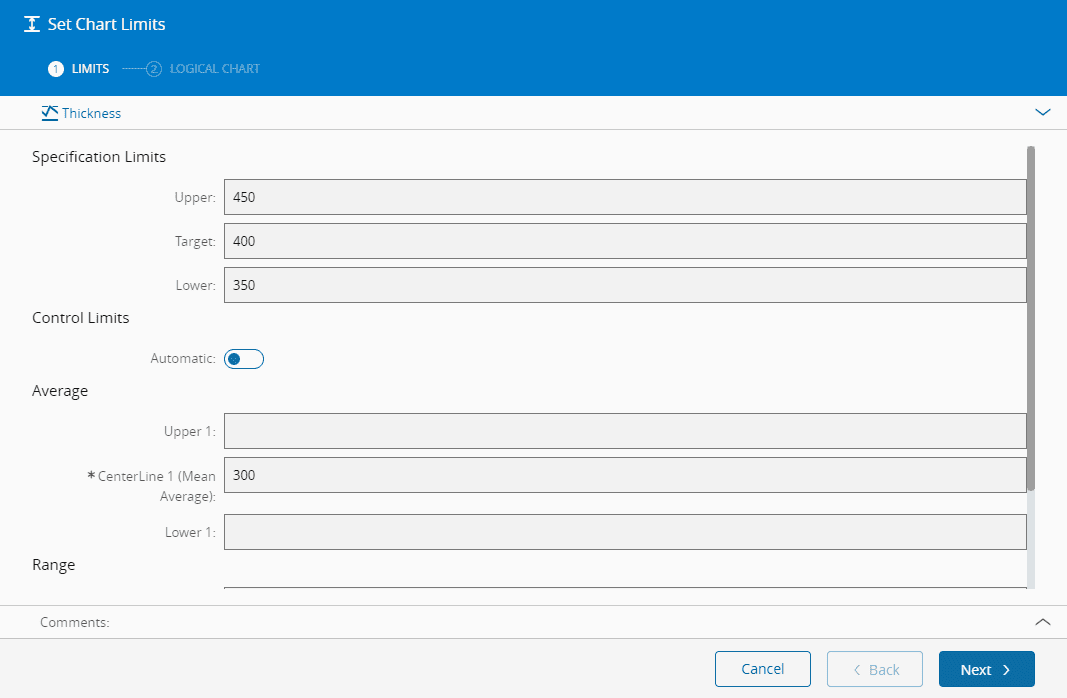
理想情况下,控制限值是根据历史数据定义的。在凯睿德MES中,当使用自动控制限值时,需要定义中心线,在变量图表中还需要定义标准偏差。使用特定于图表的统计公式,系统会根据图表类型、样本大小以及附录A - 控制图表常量中所述的控制图表常量表自动计算控制上限和下限。
也可以(但不建议)将图表配置为使用手动控制限值,在这种情况下,用户必须手动定义它们。手动定义控制限值时,可以定义指标1和指标2(用于变量图表)的控制上限、中心线和控制下限。
Info
每个逻辑控制图都有自己的控制限值,即使它们是在首次创建逻辑控制图时从原始图表复制的。
自动控制限值重新计算#
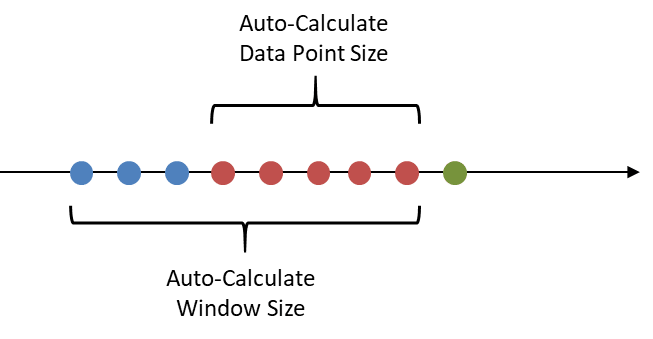
使用自动控制限值时,可以在图表级别配置每次数据点达到一定数量后必须重新计算控制限值(实际上是中心线),方法是在图表中启用自动计算选项。影响此重新计算的有两个参数:“自动计算窗口大小”(何时重新计算)和“自动计算数据点大小”(在重新计算中要考虑多少数据点),如下图所示。
系统还可以配置为只收集数据点,然后在配置了一定数量的数据点后,计算并设置中心线(以及标准偏差,如果是变量图表的话)。这可以通过在图表或逻辑控制图表中激活学习模式来实现。当激活学习模式时,还可以配置系统在一定数量的数据点后停止重新计算中心线(对于变量图表,还有标准偏差)。
Info
使用自动控制限值时,可以通过使用重新计算和设置事务,随时重新计算控制限值。
规格限制#
规格限制 - 规格上限(USL)、目标规格值(TSV)和规格下限(LSL)是顾客的呼声(VOC)。规格限制是可选的,可以为图表和每个逻辑控制图定义。
使用产品或产品组规格限制#
规格限制通常按产品或产品组定义。这种方法的优点是保持其所属的规格限制,并提供与版本控制和变更控制相关的好处。要启用产品或产品组规格限制,图表需要将产品或产品组作为上下文键。如果满足该要求,则需要将规格限制模式设置为产品。当在创建逻辑控制图时将规格限制模式设置为产品后,系统将查找与图表参数相匹配的规格类型的产品(或产品组)参数以及图表产品(或产品组)值,以自动设置规格限制。此外,如果图表将步骤定义为键,产品参数步骤也必须与图表步骤键值相匹配。
设置SPC图表#
为了设置SPC图表,有必要按照本简表中所述的步骤操作:
| 步骤 | 标题 | 描述 |
|---|---|---|
| 1 | 创建必要的参数 | 创建要控制的参数。 |
| 2 | 创建图表 | 创建SPC图表 |
| 3 | 将图表与所需的步骤和资源相关联(可选) | 使用步骤图表上下文或资源图表上下文智能表关联创建的图表。有关详细信息,请参阅步骤和资源图表上下文部分。 |
Table: SPC设置步骤
Note
参数的范围必须有数据类型十进制、持续时间或长,并且必须是EDC_SPC或EDC_SPC_Recipe。
第二步创建图表是特定于SPC的,下面将详细介绍。
创建图表#
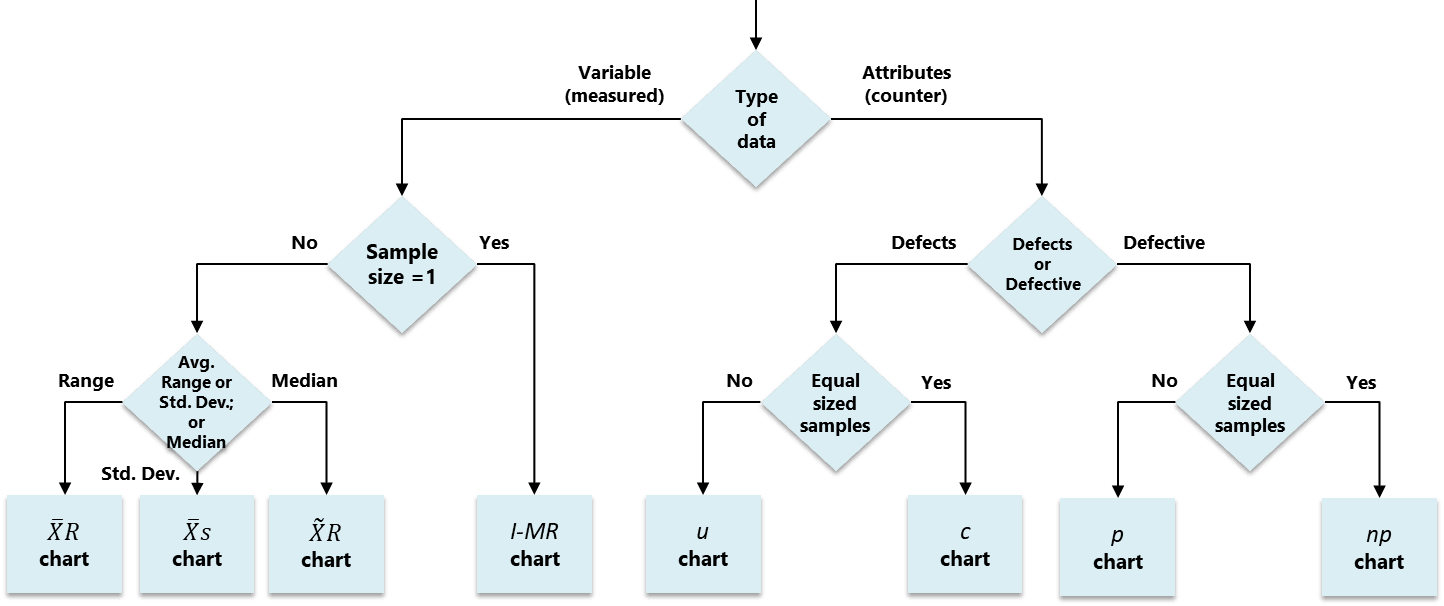
要创建图表,有必要选择适当的控制图表,下图提供了一些有关如何选择的指导。然而,最终的决定是由过程专家根据打算应用SPC控制的特定场景做出。
- 当样本大小小于4时,最好使用X̄ R图表,而不是X̄ s图表[Stapenhurst 2005]。
- 尽管当子组大小不恒定时可以使用X̄ R图表,但这并不是一个好的做法。在这些情况下,应改用X̄ s图表[Montgomery 2009]。
- 对于c图表,如果平均值较大(>5),则可以使用I-MR图表[Stapenhurst 2005]。
- 对于p图表,如果p接近0.5且n>10,则可以使用变量图表[Stapenhurst 2005]。
下表描述了不同图表创建步骤常规数据中最重要的属性:
| 属性 | 描述 |
|---|---|
| 参数 | 要由图表控制的参数 |
| 图表类型 | 图表的类型 - 系统支持四种变量图表和四种属性图表 |
| 最小样本读数 | 最小读数数量 |
| 最大样本读数 | 最大读数数量 |
| 样本读数来源 | (可选)一个查找表,从中获取读数名称以向用户显示 |
| 样本大小 | 对于具有固定样本大小的属性图表 |
| 最小样本大小 | 对于具有可变样本大小的属性图表,最小样本大小是多少 |
| 最大样本大小 | 对于具有可变样本大小的属性图表,最大样本大小是多少 |
| 终止零数据点的逻辑控制图 | 指定逻辑控制图没有数据点时是否必须自动终止 |
| 自动计算中心线 | 是否自动重新计算(控制限值所基于的)中心线。此选项只有在控制限值模式为自动时才会启用。 |
| 自动计算窗口大小 | 以发布的数据点的数量定义重新计算的频率。 |
| 自动计算窗口数据点大小 | 定义重新计算中心线(和标准偏差)时要考虑的数据点数量。 |
| 学习模式 | 图表是否在没有控制限值的情况下开始,以及是否在一定数量的数据点之后自动计算和设置限值。 |
| 学习后禁用计算 | 学习后图表是否停止重新计算中心线(和标准偏差)。 |
| 保留时间 | 定义数据点在在联机数据库中保留的小时数。 |
| 保留数据点 | 定义在线数据库中保留的数据点数量。如果超过保留时间(以小时为单位)或保留数据点,则该点会从在线数据库中移除。请注意,操作数据存储库(ODS)中仍有数据。 |
Table: SPC创建向导常规数据步骤重要属性
在下面,您可以从不同的图表创建步骤显示中看到最重要属性的描述:
| 属性 | 描述 |
|---|---|
| 默认过滤器模式 | 默认情况下,图表是显示一定数量的点还是特定的时间范围。 |
| 默认显示直方图 | 是否必须默认显示直方图 |
| 要显示的默认图形 | 对于变量图表,默认情况下是否显示指标1和/或指标2的图形 |
| 要显示的默认面板 | 要显示的默认信息面板 |
| Y轴刻度模式 | Y轴刻度是手动还是自动 |
| Y轴主要单位 | 当Y轴刻度为手动时,主要单位是什么 |
| Y轴最小值 | 当Y轴刻度为手动时,最小值是多少 |
| Y轴最大值 | 当Y轴刻度为手动时,最大值是多少 |
| 常规注释来源 | 一个查找表,在为没有违规的数据点添加注释时,用户必须从该表中选择一个值。 |
| 违规注释来源 | 一个查找表,在为有违规的数据点添加注释时,用户必须从该表中选择一个值。 |
Table: SPC创建向导显示步骤重要属性
接下来是对不同图表创建步骤限值中最重要属性的描述:
| 属性 | 描述 |
|---|---|
| 规格限制模式 | 如果上下文包括产品或产品组作为键,则可以将规格限制模式定义为产品 - 有关详细信息,请参阅使用产品或产品组规格限制部分。 |
| 规格上限 | 规格上限(可选) |
| 规格目标值 | 目标规格值(可选) |
| 规格下限 | 规格下限(可选) |
| 控制限值模式 | 控制限值是手动管理还是自动管理 |
| 控制上限1 | 指标1的控制上限。只有在控制限值模式不是自动的情况下才能指定。 |
| 中心线1 | 指标1的中心线。如果控制限值模式是自动的,则此值是必需的。 |
| 控制下限1 | 指标1的控制下限。只有在控制限值模式不是自动的情况下才能指定。 |
| 控制上限2 | 指标2的控制上限。只能在控制限值模式是手动的情况下指定。此属性仅可用于变量图表。 |
| 中心线2 | 指标2的中心线。此值只能在控制限值模式不是自动的情况下设置。此属性仅可用于变量图表。 |
| 控制下限2 | 指标2的控制下限。只有在控制限值模式不是自动的情况下才能指定。此属性仅可用于变量图表。 |
| 标准偏差 | 标准偏差的值。此属性仅适用于变量图表,如果控制限值模式为自动,则必须设置 |
Table: SPC创建向导限值步骤重要属性
在SPC创建向导的上下文步骤中,有必要指定定义每个逻辑控制图的上下文键。请记住,上下文关键值的每个唯一组合都会生成一个新的逻辑控制图。除了上下文键外,为图表定义但未标记为键的任何上下文都将被视为必要的上下文值(除了上下文键之外),在向图表发布数据时需要提供。
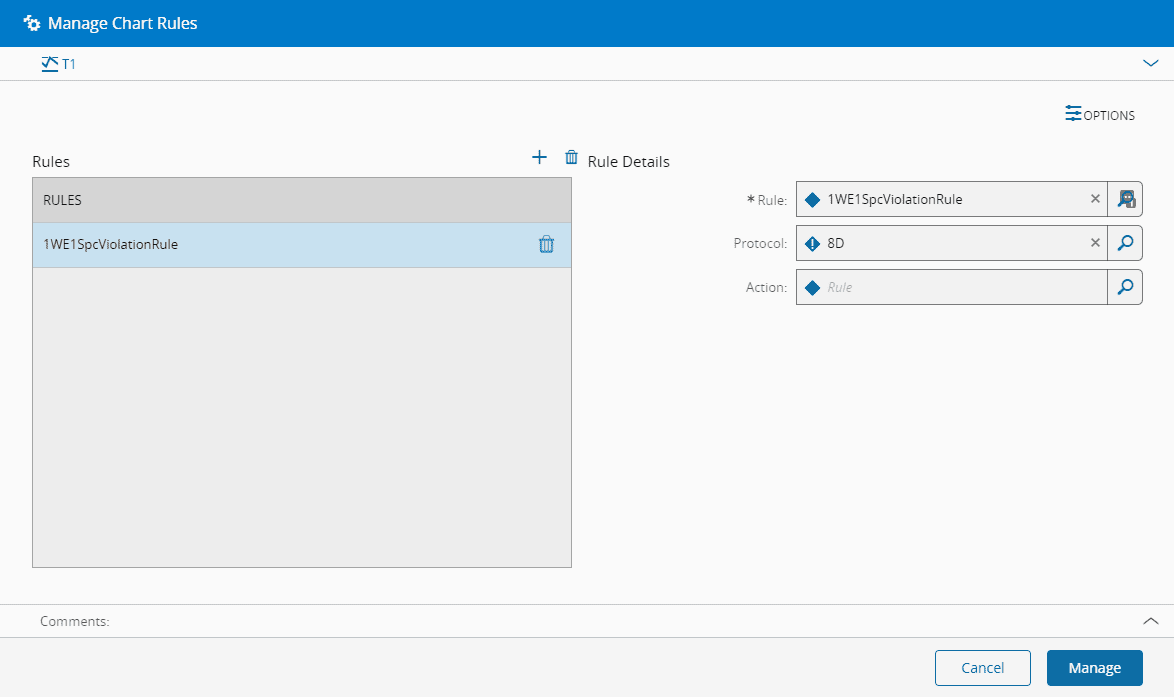
创建图表后,可以使用规则部分中提供的管理规则事务来管理规则。在管理规则事务中,如下图所示,可以添加许多SPC规则,对于每个规则,可以定义自动打开的异常处理流程,以及定义SPC操作,以便在SPC规则检测到违规时自动执行。
选项允许用户触发的处理流程指定用户是否可以手动打开与图表关联的处理流程。
创建逻辑控制图#
如前所述,每次将数据点发布到唯一的图表上下文键组合时,都会自动创建一个逻辑控制图。数据可以使用发布图表数据点或发布图表数据点汇总事务手动发布(请参阅将数据点发布到逻辑控制图),也可以通过配置数据采集以自动向SPC发送数据来自动发布数据(请参阅将数据采集与SPC集成部分)。
还可以使用管理逻辑控制图事务显式创建逻辑控制图。
设置图表限值#
使用设置图表限值事务,可以修改图表和相应逻辑控制图表的规格和控制限值。设置图表限值事务还允许修改控制限值模式,如果图表上下文键包括产品或产品组,则也可以更改规格限制模式。
- 只有在规格限制模式为图表时,才能修改规格上限、目标规格限制和规格下限
- 只有当控制限值模式设置为手动时,才能修改控制上限和控制下限。
- 还可以启用学习模式,允许用户决定是否在重新计算中心线时自动设置和使用限值。
启用或禁用图表#
可以使用启用图表和禁用图表事务启用或禁用图表。禁用图表后,无法将数据发布到其任何逻辑控制图表中。
使用SPC图表#
图表可视化#
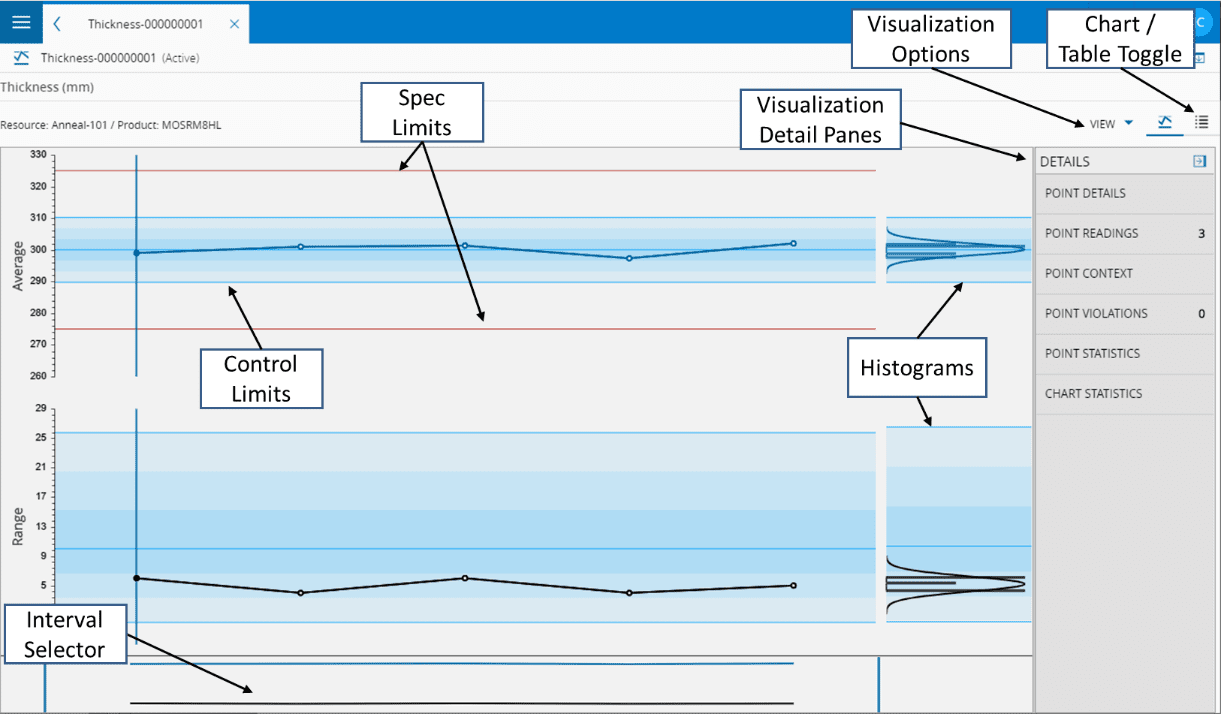
打开逻辑控制图时,系统将使用图表默认显示选项以图形方式显示该图表(有关详细信息,请参阅创建图表)。下图显示了标准图表可视化:
每个数据点的颜色和形状提供了有意义的信息,如下所示:
| 形状和颜色 | Symbol | 备注 | 排除 | 违反 |
|---|---|---|---|---|
 | 蓝色圆圈 | |||
 | 灰色圆圈 | x | ||
 | 红色圆圈 | x | ||
 | 蓝色方形 | x | ||
 | 灰色方形 | x | x | |
 | 红色方形 | x | x |
Table: 数据点形状和颜色信息
右侧有不同的详细信息面板,详见下Table:
| 面板 | 描述 |
|---|---|
| 点详细信息 | 显示有关所选数据点的信息和统计信息 |
| 点读数 | 显示所选数据点的单个读数值 |
| 点上下文 | 显示选定的数据点上下文 |
| 点违规 | 显示选定的数据点违规 |
| 点统计数据 | 显示选定的数据点统计数据 |
| 图表统计信息 | 显示考虑所有可见数据点的图表统计信息 |
Table: SPC详细信息面板
- 按下重置视图按钮可以恢复为默认视图。
- 可以通过按导出按钮将图表导出为图像或Excel表格。
下表显示了不同的图表可视化选项:
| 选项 | 描述 |
|---|---|
| 规格限制 | 显示(或隐藏)规格限制 |
| 目标值 | 显示(或隐藏)规格目标值 |
| 时间戳 | 显示(或隐藏)数据点的时间戳 |
| 直方图 | 显示(或隐藏)直方图 |
| 缩放 | 显示(或隐藏)间隔选择器 |
| 指标1 | 对于变量图表,显示(或隐藏)指标1 |
| 指标2 | 对于变量图表,显示(或隐藏)指标2 |
Table: 图表可视化选项
图表操作#
对于逻辑控制图,可以执行下表中描述的操作:
| 操作 | 描述 |
|---|---|
| 发布数据点 | 将数据点发布到逻辑控制图中。请参阅将数据点发布到逻辑控制图。 |
| 发布数据点汇总 | 通过提供摘要数据发布数据点。。请参阅将数据点发布到逻辑控制图。 |
| 重新计算并设置 | 根据历史数据重新计算和设置中心线。 |
| 转至图表定义 | 打开基本图表对象。 |
Table: 图表操作
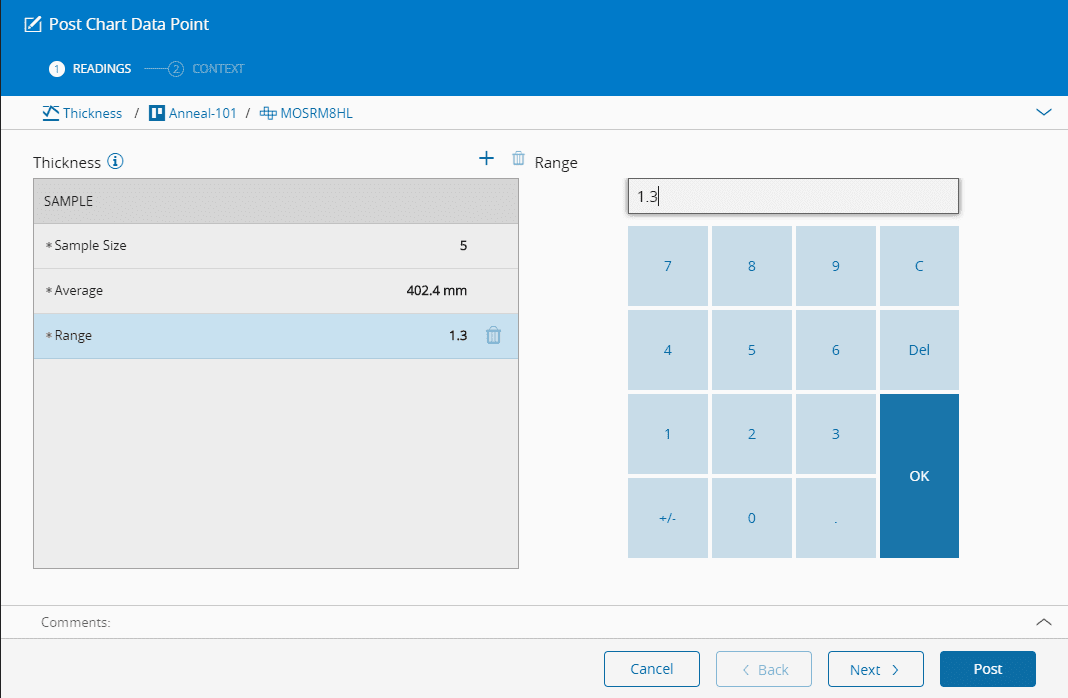
将数据点发布到逻辑控制图中#
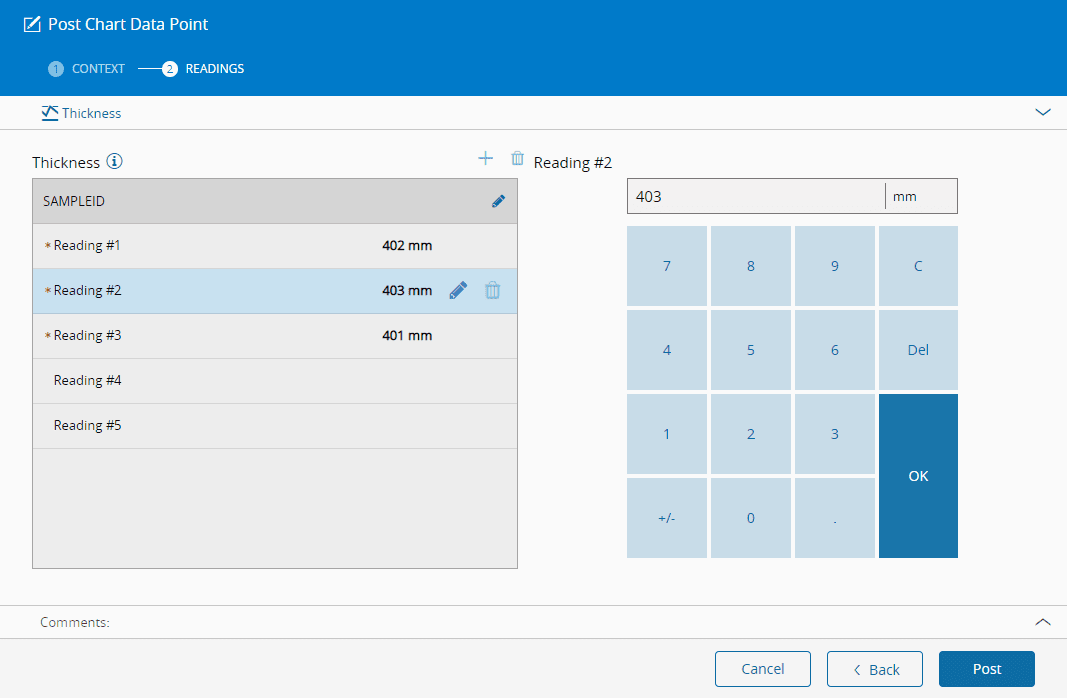
要将数据点发布到图表,有必要使用发布图表数据点事务,如下所示。发布图表数据点汇总事务可用于变量图表,它允许用户仅发布数据的摘要(样本大小、指标1值、指标2值),而不是单个的读数值,如下所示:
- 从图表调用“发布图表数据点”事务时,需要指定逻辑控制图表键。从逻辑控制图调用“发布图表数据点”事务时,上下文键会自动提供给该事务。
- 必须始终填写强制性上下文。还可以通过按“上下文”选项卡中的“添加”按钮来提供其他补充性上下文。
- 首次将数据发布到逻辑控制图时,逻辑控制图将使用该图表的默认设置自动创建。
- 如果在发布数据时输入了评论,则评论将自动与数据点关联。
- 根据为图表配置的SPC规则,如果检测到SPC违规,则可能会打开一个处理流程和/或自动执行一项SPC操作。
- 必须提供读数的值,并且必须符合图表的最小和最大读数样本大小定义。默认情况下,显示最大读数数量,强制性读数的开头标有(*)。读数的名称可以更改。
- 标准偏差值从数据点发布时的逻辑控制图标准偏差中读取。此值可能与与图表数据点统计关联的值不同。
数据点操作#
对于数据点,可以执行下表中描述的操作:
| 操作 | 描述 |
|---|---|
| 编辑 | 编辑单个数据点读数值(仅当数据点未汇总时才可能) - 当读数值被修改时,SPC规则不会运行。 - 编辑数据点时,原始数据点的适用规格限制和中心线仍将适用。 |
| 注释 | 为数据点添加注释 - 如果所选数据点没有违规,并且定义了常规注释来源,则有必要从定义的来源查找表中选择一个值。 - 如果所选数据点有违规,并且定义了违规注释来源,则有必要从定义的来源查找表中选择一个值。 |
| 排除 | 排除数据点 - 在计算控制限值时不考虑已排除和已删除的数据点。 |
| 包括 | 包括先前已排除的数据点 |
| 删除 | 从逻辑控制图中删除数据点 - 数据点一旦被删除,就无法恢复! |
| 打开处理流程 | 如果设置了允许用户触发的处理流程选项,则可以手动打开特定数据点的处理流程实例。 |
Table: 数据点操作
将数据采集与SPC集成#
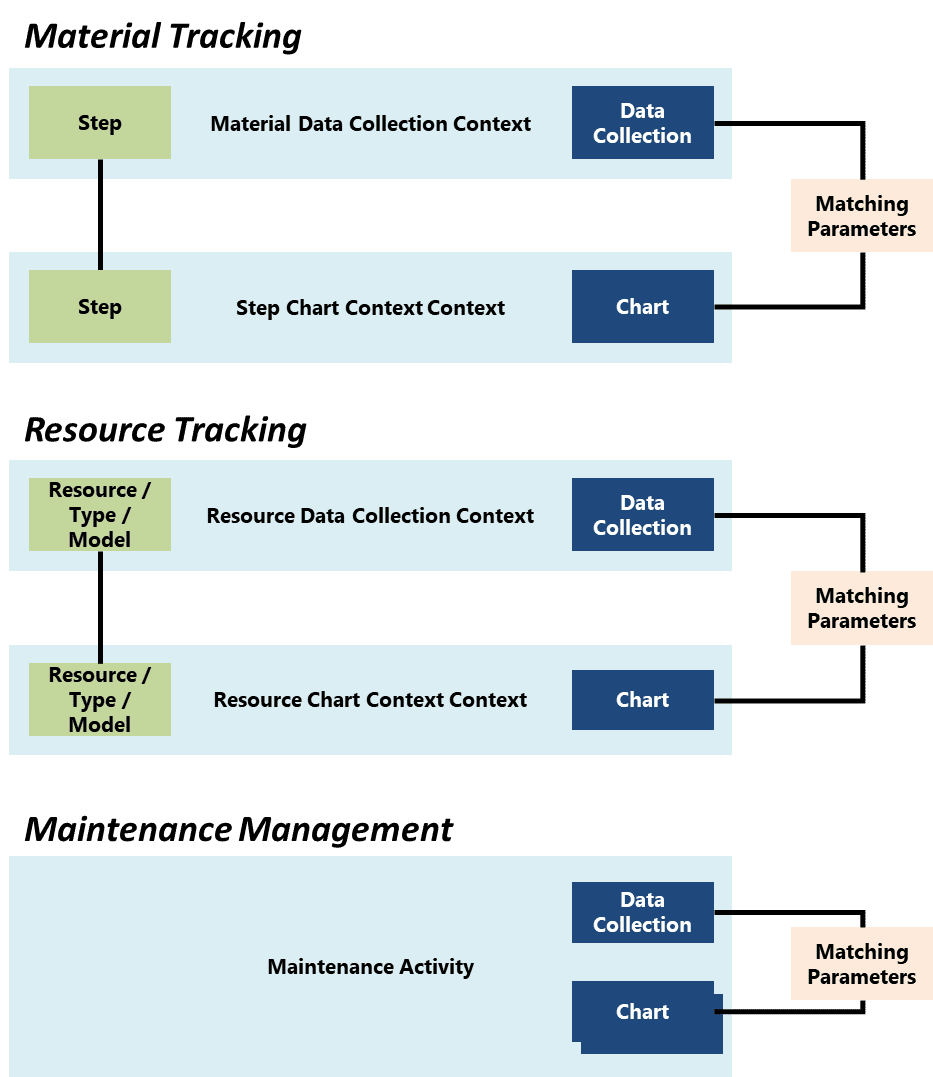
可以配置数据采集以自动将数据馈送至SPC。在物料跟踪和资源跟踪的情况下,可以通过匹配数据采集中的参数和为上下文解析的图表中的参数来实现这一点。对于物料跟踪和资源跟踪,数据采集和图表使用相同的上下文信息进行解析。对于数据采集中所有与图表参数相匹配的参数,数据将自动馈送至SPC。对于维保管理,集成是根据维保活动直接配置的。下表提供了有关如何将数据采集与SPC集成的摘要,图中提供了这种集成的说明。
| 模块 | 数据采集和SPC集成机制 |
|---|---|
| 物料跟踪 | 匹配参数位于: - 物料数据采集上下文 - 步骤图表上下文 |
| 资源跟踪 | 匹配参数位于: - 资源数据采集上下文 - 资源图表上下文 |
| 维保管理 | 通过匹配执行数据采集和关联的执行图表中的参数,执行维保活动 |
Table: 数据采集和SPC集成
Note
同一上下文中可能有许多图表。
当将数据从EDC馈送至SPC时,系统将自动为物料和资源提供尽可能多的上下文。下表列出了系统在自动从EDC向SPC发送数据时自动提供的上下文。请注意,系统上下文和图表上下文之间的上下文匹配仅由[名称]完成。
| 上下文 | 描述 | 适用于 |
|---|---|---|
| 工厂设施 | 设施名称 | 物料和资源 |
| 车间 | 区域名称 | 物料和资源 |
| 物料 | 物料名称 | 仅物料 |
| 物料类型 | 物料类型 | 仅物料 |
| 步骤 | 步骤名称 | 仅物料 |
| 资源 | 资源名称 | 物料和资源 |
| 过程资源 | 物料最后一个过程步骤资源名称 | 仅物料 |
| 产品 | 产品名称 | 仅物料 |
| 产品类型 | 产品类型 | 仅物料 |
| 产品组 | 产品组名称 | 仅物料 |
| 流程 | 流程名称 | 仅物料 |
| 物料操作 | 物料操作名称 | 仅物料 |
| 资源转换 | 资源转换名称 | 仅限资源 |
| 数据采集 | 数据采集名称 | 物料和资源 |
| 数据采集实例 | 数据采集实例ID | 物料和资源 |
Table: 提供给SPC的数据采集系统上下文
从数据采集自动向SPC发送数据时,有三种可能的模式,如下表所示。模式在数据采集级别定义,并应用于所有数据采集参数。
| 模式 | 描述 |
|---|---|
| OnPostPerSample | 每次发布数据采集样本时,都会将数据发布到SPC |
| OnClosePerSample | 只有在数据采集实例关闭时,数据才会按样本发布到SPC |
| OnClosePerParameter | 只有在数据采集实例关闭时,数据才会按参数发布到SPC(所有样本的读数都集中到单个样本中) |
Table: 提供给SPC的EDC系统上下文
Info
将数据采集数据馈送至变量图表时,数据采集参数读数的数量必须介于SPC图表的最小和最大样本大小之间。
Info
在数据采集中将数据采集数据馈送至属性图表时,要发送到SPC的参数必须将样本ID定义为样本大小,且读数数量必须为1。
Info
如果图表已禁用,数据将保存在数据采集实例中,但不会向图表发布任何数据。
Info
如果图表需要额外的强制性上下文(作为键或仅作为强制性信息),且此信息不可用,则当尝试自动将数据馈送至图表时,将抛出错误。
Info
如果在数据采集中,参数样本ID是列表或资源,则数据点样本ID将使用提供的数据采集样本ID进行设置,除非模式是OnClosePerParameter,在这种情况下,样本ID将是物料名称。
文档参考#
以下是本文档中使用的文档参考:
| 参考 | 文档 |
|---|---|
| [Cano et al. 2015] | "Quality Control with R: An ISO Standards Approach", 2015, Springer, Emilio L. Cano, Javier M. Moguerza, Mariano Prieto Corcoba |
| [Milivojevich 2015] | "Control Chart Constants -- How to Derive A2 and E2", 2015, Andrew Milivojevich |
| [Minitab 2019] | "Minitab 18 Support", 2019, Minitab LLC |
| [Montgomery 2009] | "Introduction to Statistical Quality Control" 6th Edition, 2009, John Wiley & Sons - Douglas C. Montgomery |
| [Stapenhurst 2005] | "Mastering Statistical Process Control - A Handbook for Performance Improvement Using Cases", 2005, Elsevier Butterworth-Heinemann, Tim Stapenhurst |
| [SPC For Excel] | "SPC For Excel Help", 2020, BPI Consulting |
| [Statsoft 2009] | "Statistica Help Manual", 2019, Statsoft |
| [Walker et al. 2012] | "The Certified Quality Inspector Handbook", 2012, ASQ Quality Press, H. Fred Walker, Ahmad K. ElshennawY, Bhisham C. Gupta, Mary McShane Vaughn |
Table: 文档参考
附录A - 控制图表常量#
\(c_4\)、\(c_5\)、\(d_2\)、\(d_3\)和\(e_1\)和控制图表常量列表([Cano et al.2015]、[Montgomery 2009]、[Walker et al.2012]、[Statsoft 2009]、[Milivojevich 2015])。
| 子组大小(n) | \(c_4\) | \(c_5\) | \(d_2\) | \(d_3\) | \(e_1\) |
|---|---|---|---|---|---|
| 2 | 0.797885 | 0.60281 | 1.1284 | 0.8525 | 1 |
| 3 | 0.886227 | 0.463251 | 1.6926 | 0.8884 | 1.16 |
| 4 | 0.921318 | 0.38881 | 2.0588 | 0.8798 | 1.093 |
| 5 | 0.939986 | 0.341213 | 2.3259 | 0.8641 | 1.198 |
| 6 | 0.951533 | 0.307547 | 2.5344 | 0.848 | 1.134 |
| 7 | 0.959369 | 0.282154 | 2.7044 | 0.8332 | 1.214 |
| 8 | 0.96503 | 0.262139 | 2.8472 | 0.8198 | 1.162 |
| 9 | 0.969311 | 0.245838 | 2.97 | 0.8078 | 1.223 |
| 10 | 0.972659 | 0.232238 | 3.0775 | 0.7971 | 1.174 |
| 11 | 0.97535 | 0.220663 | 3.1729 | 0.7873 | 1.228 |
| 12 | 0.977559 | 0.210662 | 3.2585 | 0.7785 | 1.188 |
| 13 | 0.979406 | 0.201901 | 3.336 | 0.7704 | 1.233 |
| 14 | 0.980971 | 0.194154 | 3.4068 | 0.763 | 1.2 |
| 15 | 0.982316 | 0.187231 | 3.4718 | 0.7562 | 1.237 |
| 16 | 0.983484 | 0.180995 | 3.532 | 0.7499 | |
| 17 | 0.984506 | 0.175351 | 3.5879 | 0.7441 | |
| 18 | 0.98541 | 0.170197 | 3.6401 | 0.7386 | |
| 19 | 0.986214 | 0.165475 | 3.689 | 0.7335 | |
| 20 | 0.986934 | 0.161125 | 3.7349 | 0.7287 | |
| 21 | 0.987583 | 0.157098 | 3.7783 | 0.7242 | |
| 22 | 0.98817 | 0.153362 | 3.8194 | 0.7199 | |
| 23 | 0.988705 | 0.149875 | 3.8583 | 0.7159 | |
| 24 | 0.989193 | 0.146619 | 3.8953 | 0.7121 | |
| 25 | 0.98964 | 0.143571 | 3.9306 | 0.7084 | |
| 26 | 0.990052 | 0.140702 | 3.965 | 0.7041 | |
| 27 | 0.990433 | 0.137994 | 3.997 | 0.7012 | |
| 28 | 0.990786 | 0.135437 | 4.028 | 0.6983 | |
| 29 | 0.991113 | 0.133023 | 4.058 | 0.6956 | |
| 30 | 0.991418 | 0.13073 | 4.086 | 0.6929 | |
| 31 | 0.991703 | 0.12855 | 4.113 | 0.6902 | |
| 32 | 0.991969 | 0.126481 | 4.139 | 0.6877 | |
| 33 | 0.992219 | 0.124505 | 4.164 | 0.6852 | |
| 34 | 0.992454 | 0.122618 | 4.189 | 0.6828 | |
| 35 | 0.992675 | 0.120815 | 4.213 | 0.6804 | |
| 36 | 0.992884 | 0.119086 | 4.236 | 0.6781 | |
| 37 | 0.99308 | 0.11744 | 4.258 | 0.6758 | |
| 38 | 0.993267 | 0.115848 | 4.28 | 0.6736 | |
| 39 | 0.993443 | 0.114328 | 4.301 | 0.6715 | |
| 40 | 0.993611 | 0.112859 | 4.322 | 0.6694 | |
| 41 | 0.99377 | 0.11145 | 4.342 | 0.6674 | |
| 42 | 0.993922 | 0.110087 | 4.361 | 0.6654 | |
| 43 | 0.994066 | 0.108779 | 4.38 | 0.6635 | |
| 44 | 0.994203 | 0.107519 | 4.398 | 0.6617 | |
| 45 | 0.994335 | 0.106292 | 4.415 | 0.6598 | |
| 46 | 0.99446 | 0.105116 | 4.432 | 0.6581 | |
| 47 | 0.99458 | 0.103974 | 4.449 | 0.6564 | |
| 48 | 0.994695 | 0.102868 | 4.466 | 0.6547 | |
| 49 | 0.994806 | 0.101789 | 4.482 | 0.6531 | |
| 50 | 0.994911 | 0.100758 | 4.498 | 0.6515 |
Table: 以下各项的常量:\(c_4\)、\(c_5\)、\(d_2\)、\(d_3\)和 \(e_1\)